Solving the Integrated Rate Law for the Association Phase.

I apologize if this is too simple a question, but I genuinely cannot solve it. I looked at the original paper ( doi.org/10.1006/abio.1993.1355 ), but every source I find skips the details.


Starting with the Rate Law

d[AB]/dt = ka*[A]*[B.]−kd*[AB]

Substitute [B.] using the mass conservation principle, and from here on let [B.] mean [B.]_Max for sake of simplicity.

d[AB]/dt = ka*[A]*([B.]-[AB])−kd*[AB]

Separation of Variables

int 1/(ka*[A]*([B.]-[AB])−kd*[AB]) d[AB] = int dt

Do a u-substitution where

u=ka*[A]*([B.]-[AB])−kd*[AB]
du = -ka*[A]−kd d[AB]

Resulting in the following Integral:

int 1/(u) * -1/(ka*[A]+kd) du = int dt

Solve the Integral:

-1/(ka*[A]+kd) * ln(u) = t

Solve for u

ln(u) = -t*(ka*[A]+kd)
u = e^(-t*(ka*[A]+kd))

Re-Substitute u

ka*[A]*([B.]-[AB])−kd*[AB] = e^(-t*(ka*[A]+kd))

Solve for [AB]

ka*[A]*[B.]-ka*[A]*[AB]−kd*[AB] = e^(-t*(ka*[A]+kd))
ka*[A]*[B.]-[AB]*(ka*[A]*+kd) = e^(-t*(ka*[A]+kd))
-[AB]*(ka*[A]*+kd) = - ka*[A]*[B.] + e^(-t*(ka*[A]+kd))
[AB]*(ka*[A]*+kd) = ka*[A]*[B.] - e^(-t*(ka*[A]+kd))
[AB] = (ka*[A]*[B.] - e^(-t*(ka*[A]+kd)))/(ka*[A]*+kd)

As you can see this doesn't match the standard equation. Working backwards, it seems like I went wrong with the u-substitution because I'm off by a factor of 1/ka*[A]*[B.] inside the natural log that is the u-substitution, but if I try to correct it then the derivative is different and that causes other problems. I can't figure out where I've gone wrong.

Any help is much appreciated.

In simpler and more abstract terms, we can say that for any system there exist a rate law such that:

d[AB]/dt = u([AB])

where the criteria for separation of variables is valid because t is not in u([AB]), thus:

int 1/u([AB]) d[AB] = int dt

If this equation is not a higher order reaction, then [AB] will not have an exponent in u([AB]), thus simple u-substitution for u([AB]) is valid because the derivative wrt [AB] will not contain [AB], thus:

int 1/u * (du/dt)^-1 du = int dt

(du/dt)^-1 int 1/u du = int dt

(du/dt)^-1 ln(u) = t

ln(u) = t(du/dt)

u = e^t(du/dt)

This should work, but it doesn't for the standard equation. So either the standard equation is wrong (unlikely), I've failed to do the math correctly, or one of my assumptions is incorrect.

I've solved it. I had forgotten to add a constant to my integral.

ln(u)+C = t(du/dt)

ln(u) = t(du/dt) - C

u = e^(t(du/dt) - C)

u = e^t(du/dt)) / e^C


ka*[A]*[B.] -[AB](ka*[A]+kd) = e^-(ka*[A]+kd)t / e^C

-[AB](ka*[A]+kd) = -ka*[A]*[B.] + e^-(ka*[A]+kd)t / e^C
[AB](ka*[A]+kd) = ka*[A]*[B.] - e^-(ka*[A]+kd)t / e^C
[AB] = [ ka*[A]*[B.] - e^-(ka*[A]+kd)t / e^C ] / [(ka*[A]+kd)]

Let C = ln(1/ka*[A]*[B.])

[AB] = [ ka*[A]*[B.] - e^-(ka*[A]+kd)t / e^ln(1/ka*[A]*[B.]) ] / [(ka*[A]+kd)]
[AB] = [ ka*[A]*[B.] - e^-(ka*[A]+kd)t / (1/ka*[A]*[B.]) ] / [(ka*[A]+kd)]
[AB] = [ ka*[A]*[B.] - ka*[A]*[B.] e^-(ka*[A]+kd)t ] / [(ka*[A]+kd)]
[AB] = ka*[A]*[B.] [ 1 - e^-(ka*[A]+kd)t ] / [(ka*[A]+kd)]
[AB] = ka*[A]*[B.]/ [(ka*[A]+kd)] [ 1 - e^-(ka*[A]+kd)t ]

I'm not sure why or how we actually know what the constant is, and I would appreciate any information on that as it seems quite relevant to applying this to different systems. Right now all I can think of is additional intuitive restrictions in the form of limits of different parts of the equation (i.e. t-->0 should make the whole equation zero, t--> infinity should make the whole equation R_eq), but I'm not sure those restrictions will be generally true (e.g. if you try to put together an equation accounting for non-specific binding. )

Hi,
I did follow your reasoning but I am not familiar with this kind of math to be of help. I can explain the reasoning about the different formulas used in SPR. Starting with the 1:1 interaction:
d[LA]/dt = ka*[L]*[A]−kd*[LA] (1)

At the beginning of an experiment (t=0) all unoccupied ligand ([L]o) is free. During the association the amount of free ligand is

[L] = [L]o – [LA]

Substitution will give

d[LA]/dt = ka*[A]*([L]o-[LA])−kd*[LA] (2)

In SPR the complex (not the ligand concentration) is measured in for instance Response/resonance units: Response R in (RU). The maximal response is equal to all occupied ligand and therefore [L]o = Rmax. And because the analyte is replenished very fast, the concentration analyte [A] = C – a constant analyte concentration.

Substitution gives

dR/dt = ka*C*(Rmax - Rt)−kd*Rt (3)

Rearanging gives

dR/dt = ka*C*Rmax – (ka*C + kd)*Rt (4)

Where dR/dt is the rate of surface complex formation and Rt is the amount of bound ligand at time t. To make things simpler you can define kobs = ka*C +kd which will give:

dR/dt = ka*C*Rmax – (kobs)*Rt (5)

Before the fast computers this was used to plot the association with ln(abs(dr/dt)) versus t which will give a line with slope kobs.

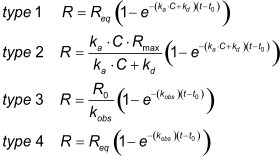
The equations 4 or 5 can be integrated which results in one of these types.